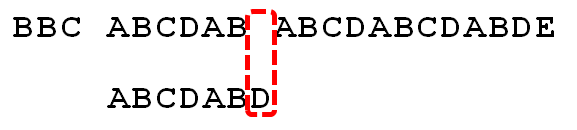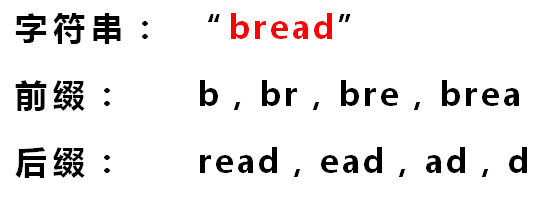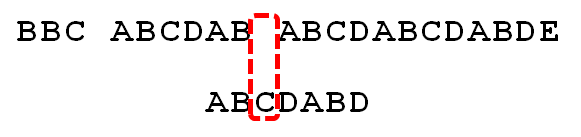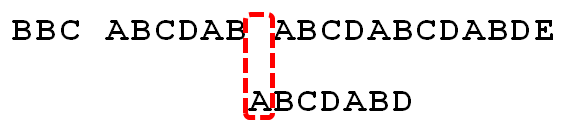字符串匹配问题又称模式匹配 (pattern matching)。该类型问题可以概括为「给定字符串 S 和 T，在主串 S 中寻找子串 T」。字符串 S 称为主串，字符串 T 称为模式串 (pattern)。

其中常见的问题有：单串匹配，即给定单个主串和模式串，找出模式串在主串中出现的所有位置；多串匹配，给定单个主串和多个模式串，找出每个模式串在主串中出现的所有位置。除此之外，还有很多匹配问题的变式，本文仅分析单串及多串匹配的基础方法和根本原理。

KMP 算法

KMP 算法是一种高效的字符串单串匹配算法，由 D.E.Knuth、J.H.Morris 和 V.R.Pratt 三人于 1977 年联合发表，故取这三人的姓氏命名。KMP 算法的时间复杂度为 \(O(n+m)\)，其中 \(n\) 为主串长度，\(m\) 为模式串长度。

暴力匹配

对于单串匹配问题，我们首先考虑最暴力的做法，穷举所有可能的起始位置，然后逐个字符进行匹配。这种方法的时间复杂度为 \(O(nm)\)，其中 \(n\) 为主串长度，\(m\) 为模式串长度。

int brute_force(string s, string t)
{
    int n = s.size(), m = t.size();
    for (int i = 0; i <= n - m; ++i)
    {
        int j = 0;
        while (j < m && s[i + j] == t[j])
            ++j;
        if (j == m)
            return i;
    }
    return -1;
}

KMP 的优化思路

时间复杂度为 \(O(nm)\) 的暴力算法显然不是我们想要的，考虑暴力算法中，我们在匹配过程中，当发生不匹配时，我们将模式串向右移动一位，然后继续匹配。这样做的问题在于，我们在匹配过程中，已经知道了前面的一部分字符是匹配的，但是我们仍然将模式串向右移动了一位，这样做是不必要的。我们可以利用已经匹配过的信息，将模式串向右移动尽可能远的距离，从而避免了一些不必要的匹配。

例如，我们考虑主串 \(s\) 为 BBC ABCDAB ABCDABCDABDE，模式串 \(t\) 为 ABCDABD。当发生了不匹配时，暴力算法会将模式串向右移动一位，继续匹配。但是我们已经知道，前面的 ABCDAB 是匹配的，所以我们可以将模式串向右移动，从而避免了一些不必要的匹配。

这个移动的距离，就是 ABCDAB 这个字符串的「最长公共前后缀」的长度。从集合的角度去理解，就是将一个字符串的所有前缀和所有后缀视为两个集合，取交集后，其中长度最长的即为「最长公共前后缀」

ABCDAB 的最长公共前后缀是 AB，长度为 2，因此可以向右移动 「已匹配的字符串长度 - 最长公共前后缀长度」的距离。

此时，C 与空格又失配了，已匹配的字符串是 AB，其最长公共前后缀长度为 0，所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

如此模拟，即可达成快速匹配的优化。而「最长公共前后缀」的求解，我们下面引入「前缀函数」的概念。

前缀函数

给定一个长度为\(n\)的字符串\(s\)（下标从\(1\)开始），约定\(s[l,r]\)表示从\(s[l]\)开始到\(s[r]\)结束的字符串。我们形式化地定义一个字符串 \(s\) 的「最长公共前后缀」为「前缀函数」\(\pi\)，其中 \(\pi[i]\) 表示字符串\(s[1,i]\)的最长公共前后缀的长度。

若\(\pi[i]=j\)，则有字符串\(s[1,j]=s[i-j+1,i]\)。数学定义即为：\(\pi(i)=max\{j|s[1,j]=s[i−j+1,i], j < i\}\) 。需要注意的是，数学定义中，\(j\)的取值范围为\([1,i)\)，而不是\([0,i)\)，因为我们不考虑\(s[1,i]\)本身，即我们考虑的前后缀为真前后缀。

前缀函数的性质与求解

根据定义，我们能够推导出两个结论来帮助我们快速求解\(\pi\)函数。

第一个性质

\(\pi[i+1] \le \pi [i] + 1\)

证明这个结论，我们不妨利用反证法。

假设\(\exists i \in [1,n)\)，满足\(\pi[i+1]>\pi[i]+1\)。

依据\(\pi[i+1]\)的定义，有\(s[1,j] = s[i-j+2,i+1]\)，对于等式两边的字符串同时删去最右边的一个字符，有\(s[1, \pi[i+1]-1]=s[i-\pi[i+1]+2,i]\)。那么，\(s[1,\pi[i+1]-1]\)是\(s[1,i]\)的真前缀，同时也是\(s[1,i]\)的真后缀。由于定义中\(\pi[i]\)是\(s[1,i]\)的最长真前缀，而假设中\(\pi[i+1]-1>\pi[i]\)，两者矛盾，所以假设不成立。

第二个性质

观察第一个性质, 考虑不等式的等号可以何时取得:

若\(s[i+1]=s[\pi[i]+1]\), 则有\(\pi[i+1]=\pi[i]+1\)

这个结论可以比较形象地去理解：\(s[1,\pi[i]]=s[i-\pi[i]+1,i]\)，两个字符串右边界同时囊括新的元素, 左侧字符串加入的是\(s[\pi[i]+1]\)，右侧加入的是\(s[i+1]\)，由于\(s[i+1]=s[\pi[i]+1]\)，所以等式\(s[1,\pi[i]+1]=s[i-\pi[i]+1,i+1]\)成立。根据性质一，此时构造出的公共前后缀长度（\(\pi[i]+1\)）已取得最大值，所以\(\pi[i+1]=\pi[i]+1\)。

前缀函数的求解

由于第二个性质是递推关系的，所以我们可以利用这个重新描述一下\(\pi[i+1]\)的定义，让其更便于计算。

找到最大的\(j\), 使得\(s[1, j]=s[i-j+1,i]\)且\(s[i]=s[j+1]\), 此时由第二个性质可得\(\pi[i+1]=j+1\)

求解这个定义式，我们可以从后往前考虑，假设我们已经求出了\(\pi[i]\)，我们考虑如何求解\(\pi[i+1]\)。我们可以将\(s[i+1]\)与\(s[\pi[i] + 1]\)进行比较，如果相等，那么\(\pi[i+1]=\pi[i]+1\)。

如果不相等，我们需要在 \(s[1,i+1]\) 中找到一个真前缀，满足\(s[1,j]=s[i-j+2,i+1]\)，且\(s[i+1]=s[j+1]\)。我们可以利用\(\pi\)函数的性质，将\(j\)向前移动，直到找到一个满足条件的\(j\)，或者\(j=0\)。如果\(j=0\)，那么\(\pi[i+1]=0\)。

KMP 算法的实现

根据前缀函数的定义，我们将主串拼接到模式串后面, 那么这个新串的长度为\(m\)的前缀就是模式串, 对这个新的字符串求前缀函数, 若\(\pi[i]=m\), 则出现一次模式串完全匹配. 在两串中间添加的分隔符是为了保证新串的前缀函数不会大于模式串的长度。这样做的好处是，我们可以将模式串和主串的前缀函数求解过程统一起来，从而简化代码。

#include <bits/stdc++.h>
using namespace std;
const int M = 200010;
char s[M], p[M];
int n, m, ne[M];
int main()
{
    scanf("%d%s%d%s", &n, p + 1, &m, s);
    p[n + 1] = '#';
    strcat(p + 1, s);
    int len = strlen(p + 1);
    for (int i = 2; i <= len; i++)
    {
        int j = ne[i - 1];
        while (j && p[j + 1] != p[i])
            j = ne[j];
        if (p[j + 1] == p[i])
            j++;
        ne[i] = j;
        if (ne[i] == n)
            printf("%d ", i - n - n - 1);
    }
    return 0;
}

例题

CF1137B-Camp schedule

题意

给定\(01\)字符串\(s\)和\(t\), 重新组合\(s\)内元素的位置, 使得\(t\)能够尽可能多的在\(s\)中匹配, 输出重新构造后的\(s\)

分析

朴素想法是先统计\(s\)内的\(0,1\)数量\(cnt[0],cnt[1]\), 将\(t\)尽可能多的循环输出, 直至无法构成\(t\)后输出剩余的\(0\)和\(1\), 但是由于匹配是可以允许又重叠部分的, 如\(101\)在\(10101\)中匹配了两次. 考虑贪心的思想, 我们要想匹配尽可能多, 就要让匹配之间的重叠部分尽可能大, 而匹配之间存在的最大重叠就是\(t\)的最长公共前后缀, 随后想到\(KMP\)算法.

我们首先判断\(s\)的元素能否构造出一个\(t\), 不能就直接返回\(s\), 可以就令\(ans=t\), 而后从\(t\)的第二位开始匹配\(t\).

我们记录当前\(t\)匹配到的位置\(pos\), 此时如果还有该位置需要的元素就令\(ans+=t[pos],cnt[t[pos]]--\). 如果匹配到了\(t\)的末尾, 令\(pos=ne[pos]\), 表示重新开始新一轮匹配. 循环直到\(s\)内元素用完或者无法继续匹配了, 将剩余的元素加到\(ans\)后面即可.

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 500010;
char s[N], t[N];
int ne[N];
string res;
int cnt[2];
int main()
{
    scanf("%s%s", s + 1, t + 1);
    int ls, lt;
    ls = strlen(s + 1), lt = strlen(t + 1);
    if (ls < lt)
    {
        printf("%s\n", s + 1);
        return 0;
    }
    for (int i = 1; i <= ls; i++)
        cnt[s[i] - '0']++;
    for (int i = 2; i <= lt; i++)
    {
        int j = ne[i - 1];
        while (t[i] != t[j + 1] && j)
            j = ne[j];
        if (t[i] == t[j + 1])
            ++j;
        ne[i] = j;
    }
    int len = 1;
    while (cnt[0] > 0 && cnt[1] > 0)
    {
        if (t[len] == '0')
        {
            if (cnt[0] > 0)
            {
                res += '0';
                cnt[0]--;
            }
            else
                break;
        }
        else
        {
            if (cnt[1] > 0)
            {
                res += '1';
                cnt[1]--;
            }
            else
                break;
        }
        len++;
        if (len == lt + 1)
            len = ne[lt] + 1;
    }
    while (cnt[0]--)
        res += '0';
    while (cnt[1]--)
        res += '1';
    cout << res << endl;
    return 0;
}

CF535D-Tavas and Malekas

题意

已知字符串 \(p\) 是一个长度为 \(n\) 的字符串的子串, 给定 \(p\) 在原串中匹配的 \(m\) 个位置, 求解原字符串可能有多少种情况.

分析

若无条件限制, 总可能方案数是 \(26^n\) , 根据题意, 我们统计在满足条件后原串中已经固定了字符的数量 \(cnt\) , 答案就是 \(26^{n-cnt}\) 中方案数.

考虑暴力枚举, 时间复杂度为 \(\mathcal{O}(n^2)\) 会 TLE, 所以使用 \(KMP\) 内前缀数组的思想进行优化.

在枚举 \(m\) 个位置的时候考虑两种情形, 1）枚举两个位置中间的长度大于等于 \(|p|\) 的长度, 那么直接使这 \(|p|\) 个位置固定, 2）枚举两个位置中间的长度小于 \(|p|\) , 则考虑利用前缀数组将字符串 \(p\) 当前填充的位置向后移动, 若无法通过移动满足条件就输出 0, 否则就将这中间一段也加进 \(cnt\) , 最终复杂度 \(\mathcal{O}(n+m)\) .

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
int n, m, x[N], ne[N], cnt;
char p[N];

long long qmi(long long a, long long b, long long m)
{
    a %= m;
    long long res = 1;
    while (b > 0)
    {
        if (b & 1)
            res = res * a % m;
        a = a * a % m;
        b >>= 1;
    }
    return res;
}

int main()
{
    cin >> n >> m >> p + 1;
    for (int i = 1; i <= m; i++)
        cin >> x[i];
    int len = strlen(p + 1);
    for (int i = 2; i <= len; i++)
    {
        int j = ne[i - 1];
        while (p[j + 1] != p[i] && j)
            j = ne[j];
        if (p[j + 1] == p[i])
            ++j;
        ne[i] = j;
    }
    sort(x + 1, x + m + 1);
    for (int i = 1; i <= m; i++)
    {
        if (i == 1 || x[i] - x[i - 1] >= len)
        {
            cnt += len;
        }
        else
        {
            bool flag = false;
            int j = ne[len], l = x[i - 1] + len - x[i];
            while (j)
            {
                if (j == l)
                {
                    flag = true;
                    cnt += len - l;
                    break;
                }
                j = ne[j];
            }
            if (!flag)
            {
                puts("0");
                return 0;
            }
        }
    }
    printf("%lld\n", qmi(26, n - cnt, 1000000007));
}

CF149E-Martian String

题意

给定字符串\(s\)和若干个字符串\(p\), 求满足\(\exists a,b,c,d,(1 \le a \le b \le c \le d \le |s|)\), 使得\(s[a,b]+s[c,d]=p\)的\(p\)串个数.

分析

对于每一个\(p\)串进行判断, 首先找到\(p\)的所有真前缀在\(s\)中的第一次匹配, 记录每个匹配内最后一个字母的位置\(pre[i]\)（\(i\)表示当前前缀的长度）, 如果无法匹配则默认为\(1\). 然后将\(s,p\)都反转过来, 找到所有当前的\(p\)的真前缀的第一次匹配, 比较此时第一个字母的位置和\(pre[len - i]\), 如果合法, 那么判断该串满足条件, 如果所有真前缀都不满足, 则不满足条件.

之所以记录第一次匹配是为了尽可能的去满足\(s[a,b],s[c,d]\)两子串不重叠的条件, 如果第一次都要产生重叠, 那么接下来的就更不可能了.

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 1010;
char s[N], p[M], sr[N], pr[M];
int pre[M], suf[M], ne[M];
int res = 0;

int main()
{
    scanf("%s", s + 1);
    int m;
    scanf("%d", &m);
    int ls = strlen(s + 1);

    for (int i = ls, j = 1; i > 0; i--)
        sr[j++] = s[i];
    while (m--)
    {
        scanf("%s", p + 1);
        int len = strlen(p + 1);
        if (len < 2)
            continue;

        memset(pre, 0, sizeof pre);
        memset(suf, 0, sizeof suf);
        int j = 0;

        for (int i = 2; i <= len; i++)
        {
            while (j && p[i] != p[j + 1])
                j = ne[j];

            if (p[i] == p[j + 1])
                j++;

            ne[i] = j;
        }
        j = 0;
        for (int i = 1; i <= ls; i++)
        {

            while (j && s[i] != p[j + 1])
                j = ne[j];

            if (p[j + 1] == s[i])
                j++;

            if (!pre[j])

                pre[j] = i;
            if (j == len)
                break;
        }

        for (int i = len, k = 1; i > 0; i--)
            pr[k++] = p[i];
        memset(ne, 0, sizeof ne);

        j = 0;
        for (int i = 2; i <= len; i++)
        {

            while (j && pr[i] != pr[j + 1])
                j = ne[j];

            if (pr[i] == pr[j + 1])
                j++;

            ne[i] = j;
        }
        j = 0;
        for (int i = 1; i <= ls; i++)
        {

            while (j && sr[i] != pr[j + 1])
                j = ne[j];

            if (pr[j + 1] == sr[i])
                j++;

            if (!suf[j])

                suf[j] = i;
            if (j == len)
                break;
        }

        for (int i = 1; i < len; i++)
        {
            if (pre[i] && suf[len - i] && pre[i] < ls - suf[len - i] + 1)
            {
                res++;
                break;
            }
        }
    }
    printf("%d\n", res);
    return 0;
}

AC 自动机

AC 自动机是一种高效的字符串多串匹配算法，由 Aho、Corasick 两人于 1975 年发表，故取两人的姓氏命名。AC 自动机的时间复杂度为 \(O(n+m)\)，其中 \(n\) 为主串长度，\(m\) 为模式串总长度。

Trie 树

在介绍 AC 自动机之前，我们需要先了解一下，什么是 Trie 树。Trie 树是一种高效的字符串存储结构，其时间复杂度为 \(O(n)\)，其中 \(n\) 为字符串长度。Trie 树的基本思想是，将字符串看作是一棵树，字符在边上，每个节点表示一个字符串的前缀（后文也会将节点称为一个状态），从根节点到叶子节点的路径表示一个字符串，从一个节点到根节点的路径可以表示字符串的一个前缀，从一个节点到含有结束标记的节点的路径可以表示字符串的一个后缀。Trie 树的每个节点包含若干个指向子节点的指针，每个节点的子节点的个数等于字符集的大小。Trie 树的根节点表示空串，每个节点的深度为该节点所表示的前缀的长度。

const int N = 5e5 + 10, M = 1e6 + 10;
int trie[N][26], cnt[N];
char str[M];
void insert()
{
    int p = 0;
    for (int i = 1; str[i]; i++)
    {
        int c = str[i] - 'a';
        if (!trie[p][c])
            trie[p][c] = ++idx;
        p = trie[p][c];
    }
    cnt[p]++;
}

基本思想

AC 自动机是基于 Trie 树的数据结构利用 KMP 的思想进行多模式匹配的算法。其与 KMP 算法的不同之处仅仅在于，前缀函数的求解方式不同。KMP 算法中，我们是在模式串上求解前缀函数，而 AC 自动机中，我们是在 Trie 树上求解前缀函数。

粗略地理解，就是把一堆模式串合成一棵树，让原串和一棵树去匹配，匹配过程中，利用类似最长公共前后缀的思想来加速，获得平均线性的复杂度。差异就在于，KMP 算法求的是最长公共前后缀，而 AC 自动机中，对于一个后缀，并不关心前缀是否与该后缀来源自一个模式串。

失配指针

对于若干个模式串 \(s_1,s_2\dots s_n\)，将它们构建一棵字典树后的所有状态的集合记作 \(Q\)。AC 自动机利用一个 fail 指针来辅助多模式串的匹配。状态 \(u\) 的 fail 指针指向另一个状态 \(v\)，其中 \(v\in Q\)，且 \(v\) 是 \(u\) 的最长后缀（即在若干个后缀状态中取最长的一个作为 fail 指针）。根据上文对 Trie 的介绍，节点表示字符串的前缀，此处的 \(v\) 就是与 \(u\) 的最长后缀相等的前缀。

构建 fail 指针，可以参考 KMP 中求解前缀函数的思想，类似于一维推广至二维。考虑字典树中当前的结点 \(u\)，\(u\) 的父结点是 \(p\)，\(p\) 通过字符 c 的边指向 \(u\)，即 \(trie[p,\mathtt{c}]=u\)。假设深度小于 \(u\) 的所有结点的 fail 指针都已求得。

1. 如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 存在：则让 u 的 fail 指针指向 \(\text{trie}[\text{fail}[p],\mathtt{c}]\)。相当于在 \(p\) 和 \(\text{fail}[p]\) 后面加一个字符 c，分别对应 \(u\) 和 \(fail[u]\)。
2. 如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 不存在：那么我们继续找到 \(\text{trie}[\text{fail}[\text{fail}[p]],\mathtt{c}]\)。重复 1 的判断过程，一直跳 fail 指针直到根结点。
3. 如果真的没有，就让 fail 指针指向根结点。

如此即完成了 \(\text{fail}[u]\) 的构建。

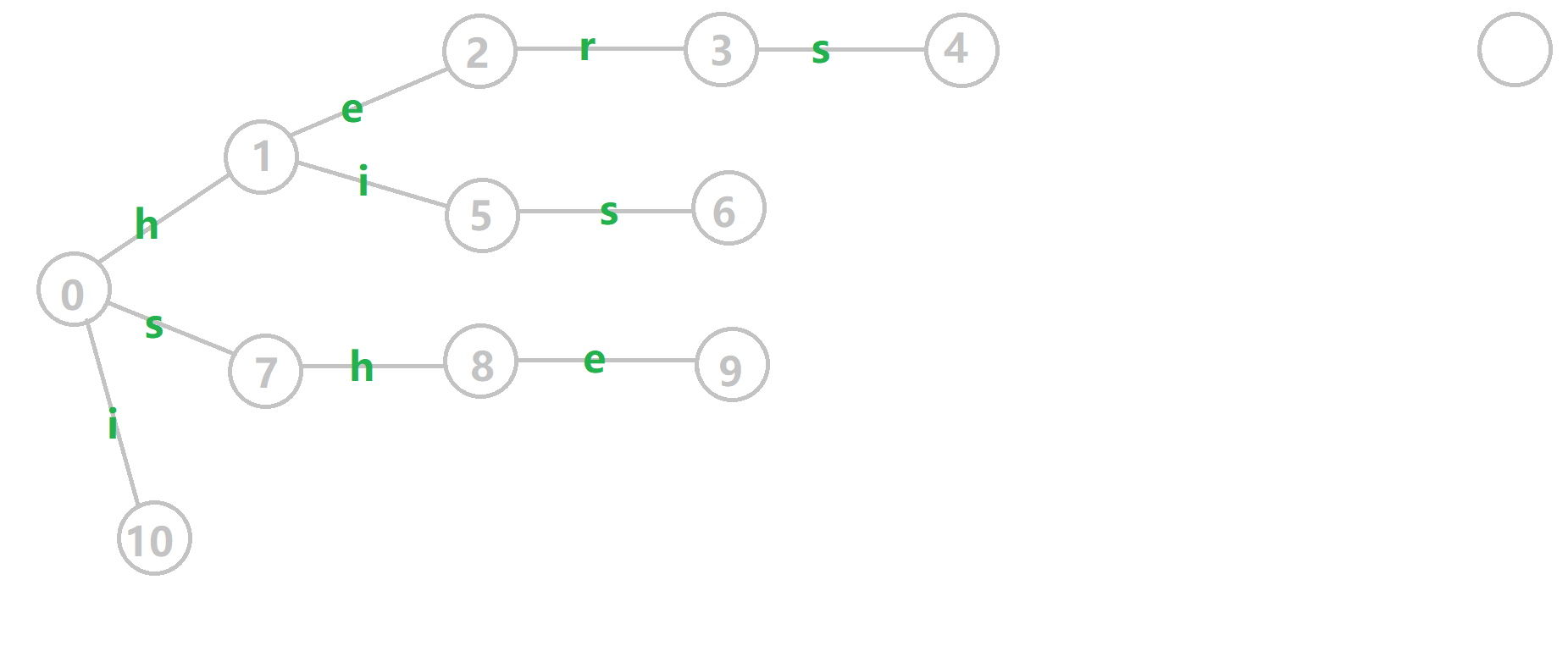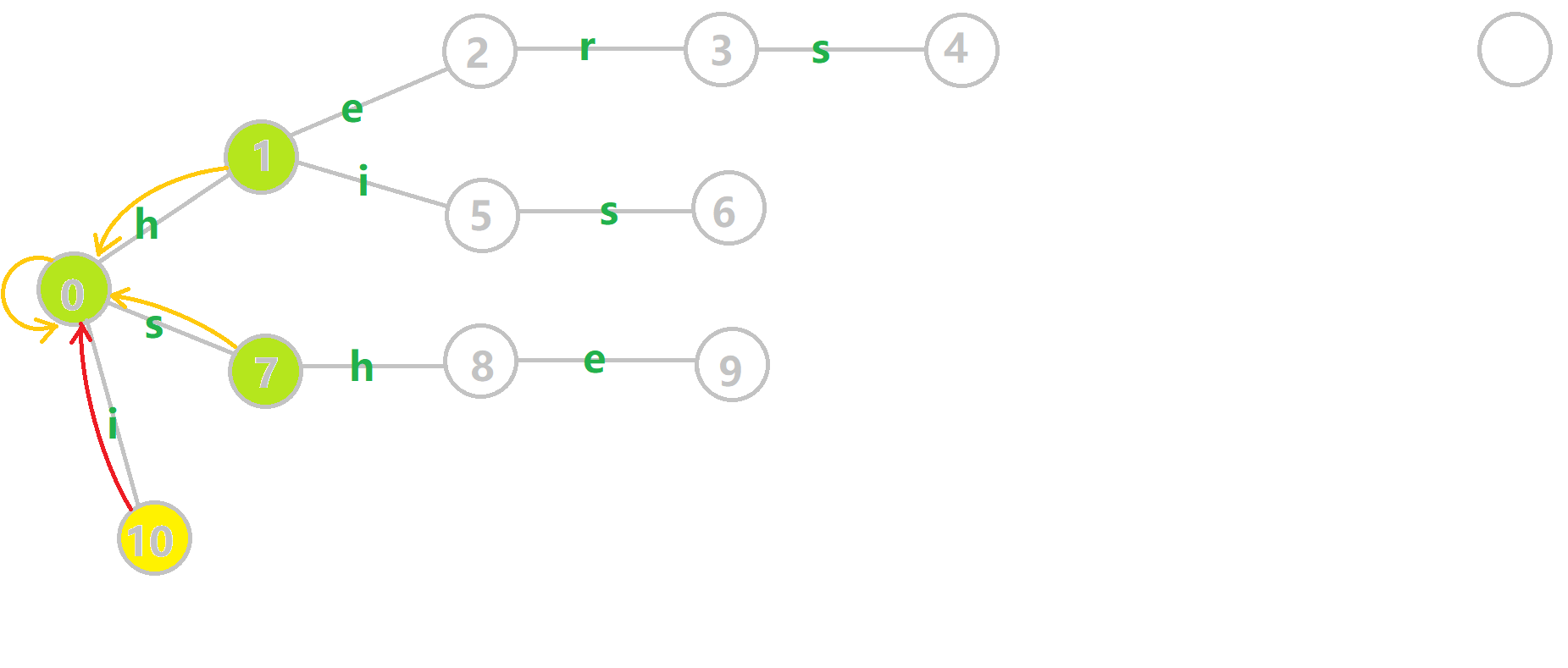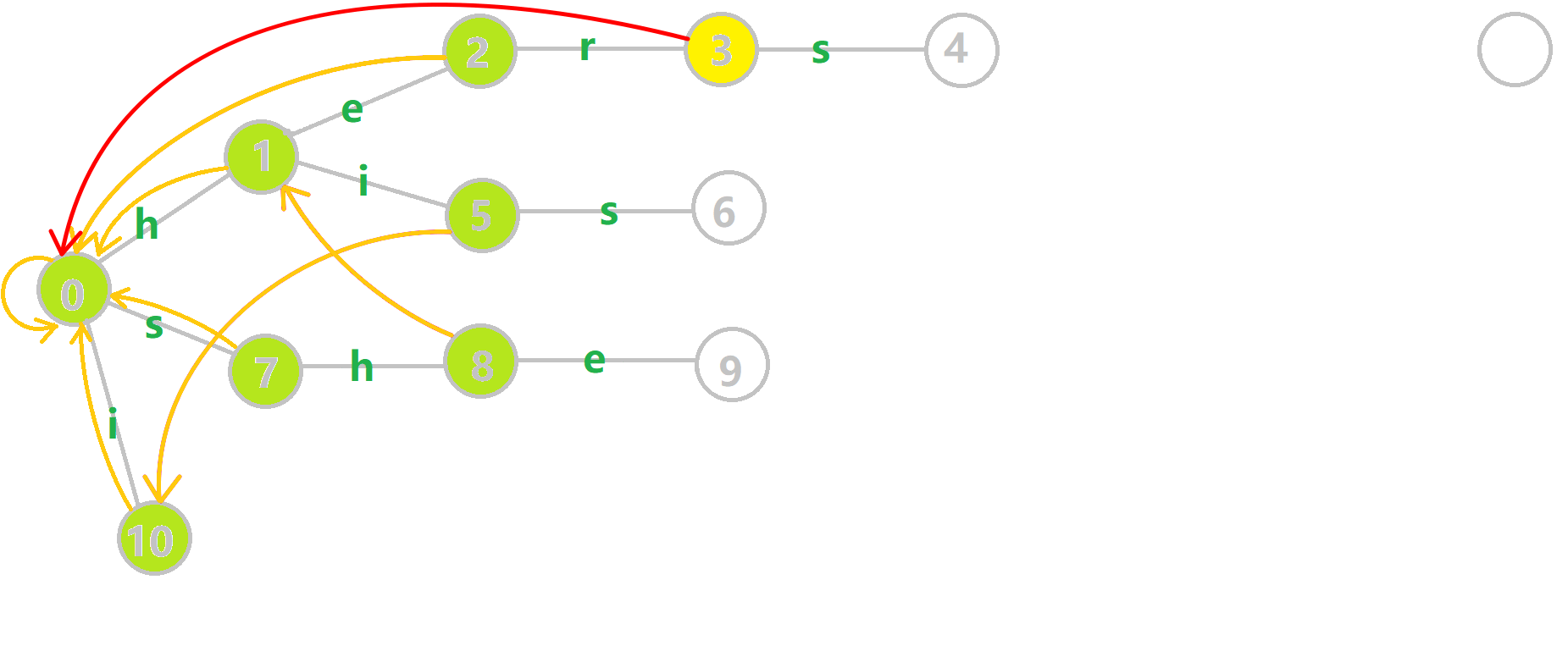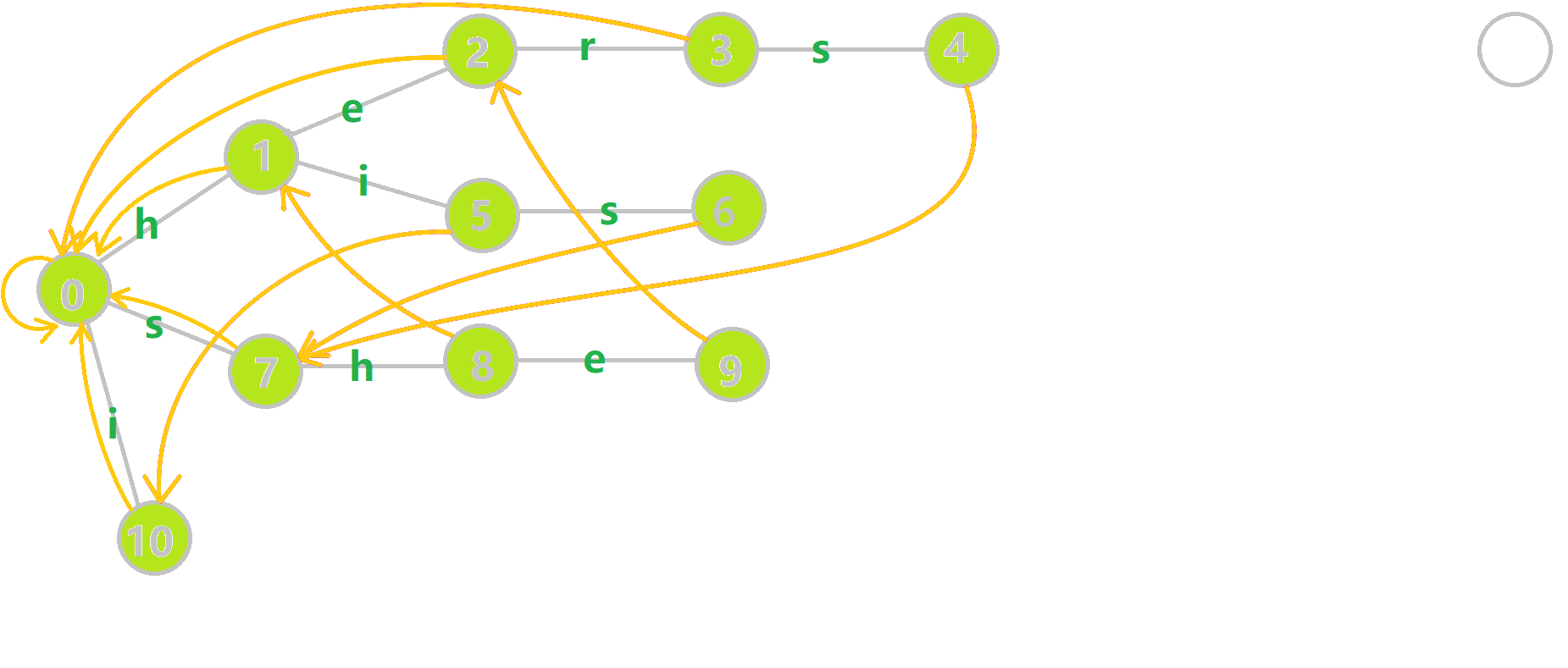
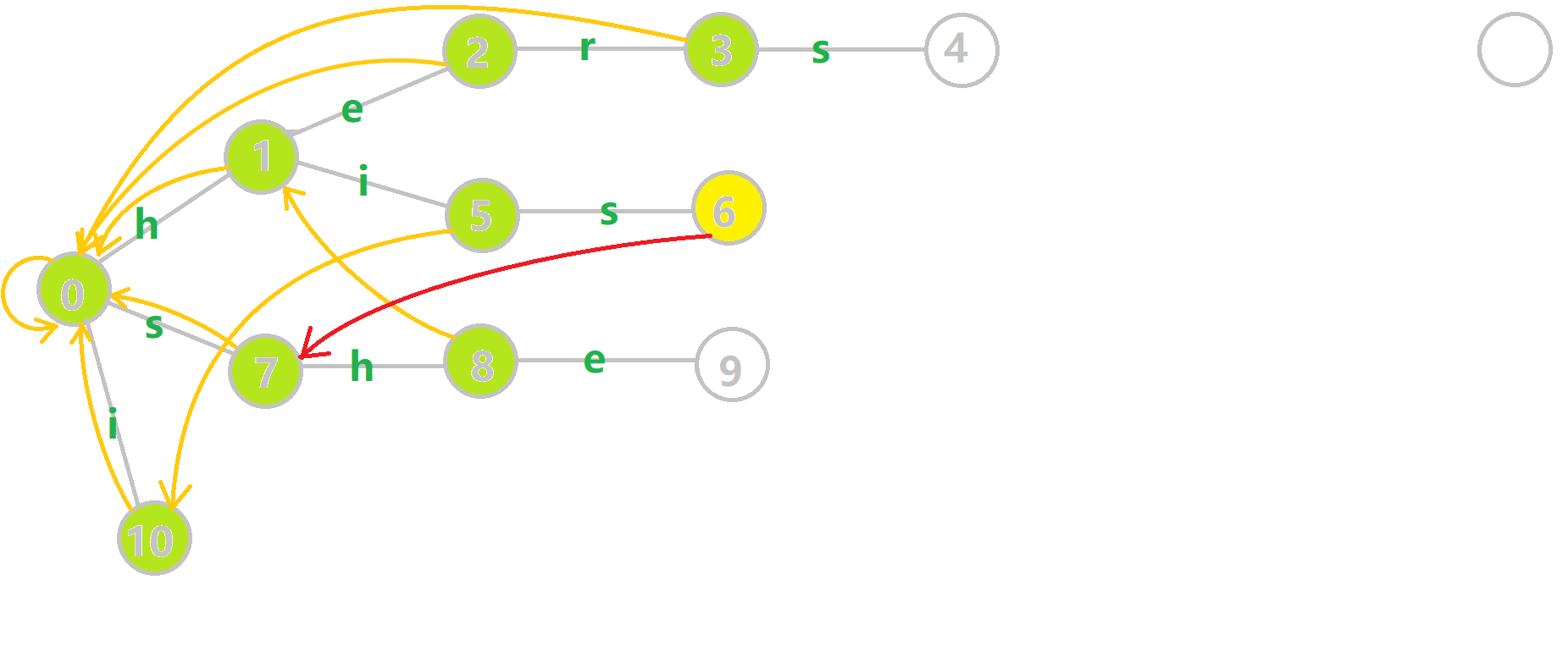
OI-Wiki 上的例子可以很好的帮助理解构建过程。对字符串 i he his she hers 组成的字典树构建 fail 指针：

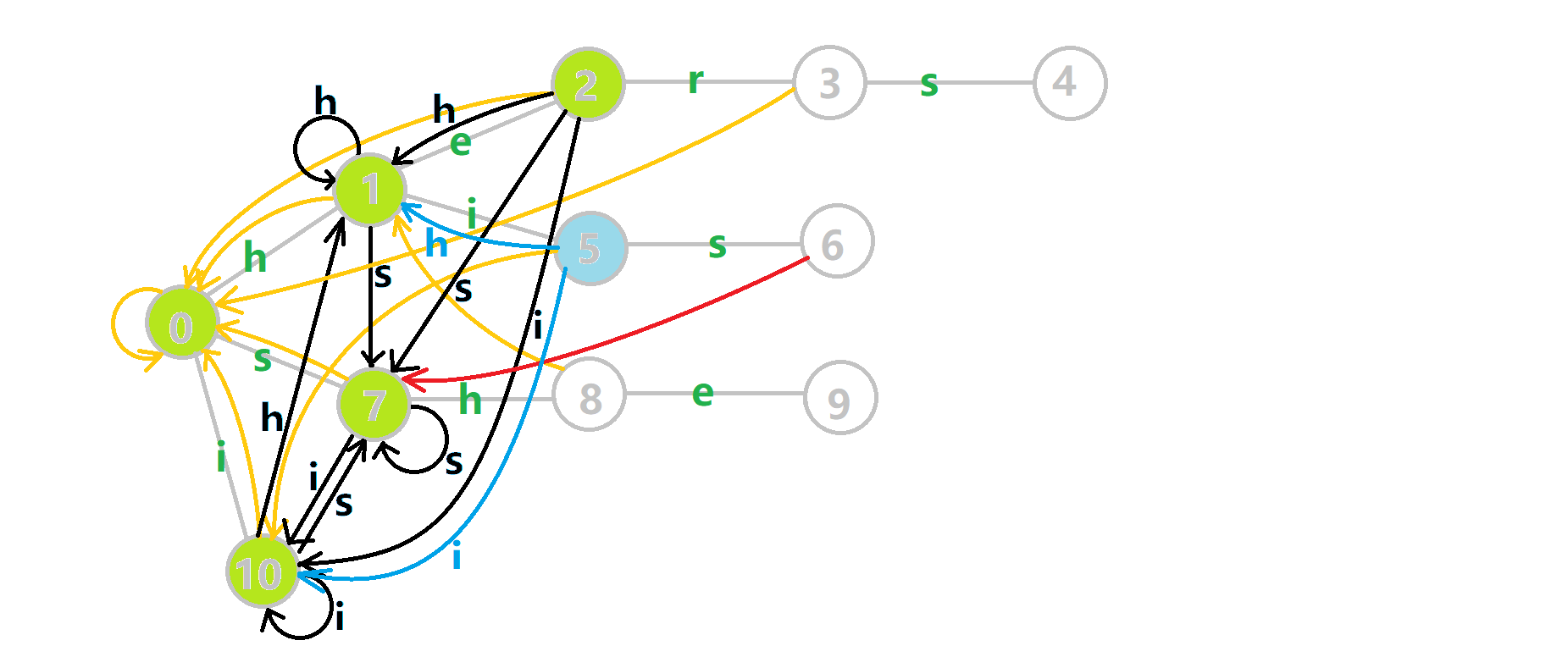
1. 黄色结点：当前的结点 \(u\)。
2. 绿色结点：表示已经 BFS 遍历完毕的结点，
3. 橙色的边：fail 指针。
4. 红色的边：当前求出的 fail 指针。

我们重点分析结点 6 的 fail 指针构建：

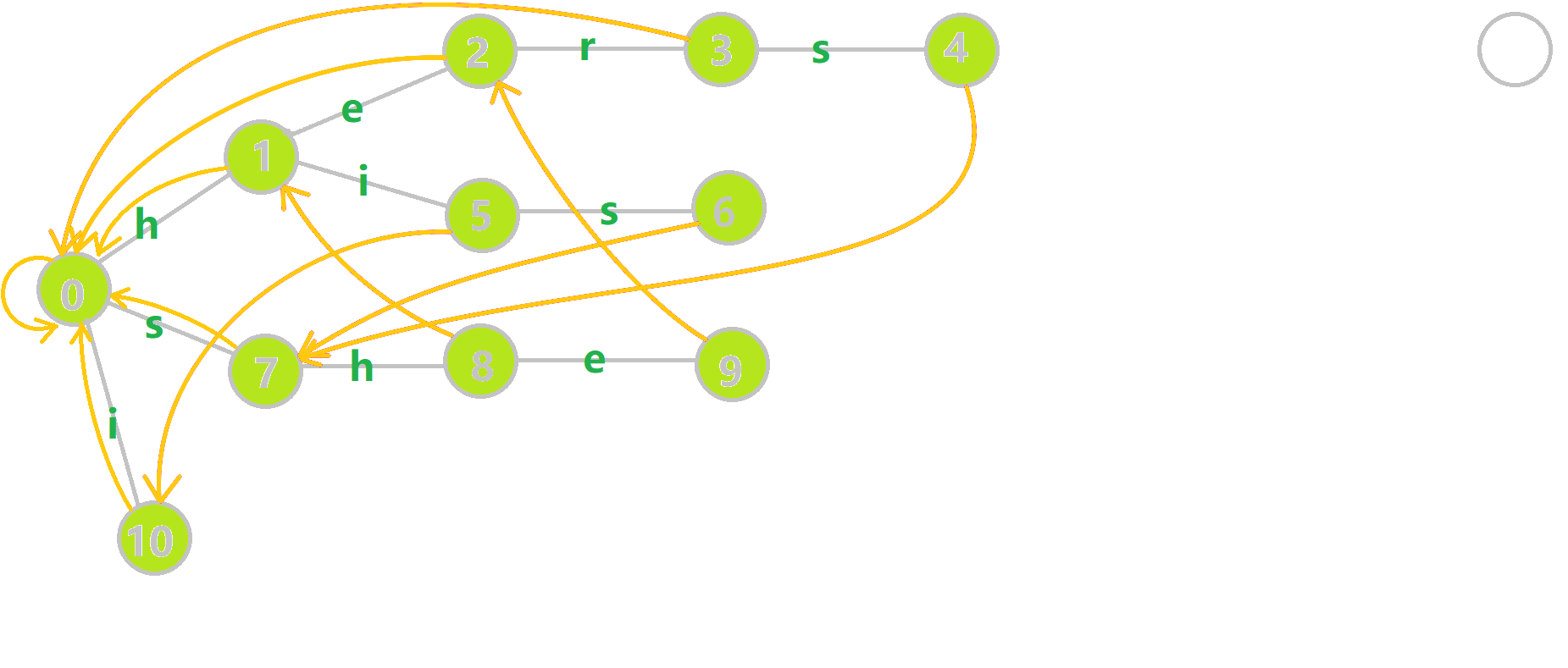
找到 6 的父结点 5，\(\text{fail}[5]=10\)。然而 10 结点没有字母 s 连出的边；继续跳到 10 的 fail 指针，\(\text{fail}[10]=0\)。发现 0 结点有字母 s 连出的边，指向 7 结点；所以 \(\text{fail}[6]=7\)。最后放一张建出来的图：

AC 自动机的实现

依据基本思路，失配指针的求解依赖于深度小于当前求解节点的失配指针，所以我们需要按照深度从小到大的顺序求解失配指针。我们可以利用 BFS 的思想，从根结点开始，依次求解深度为 \(d\) 的所有结点的失配指针，直到所有结点的失配指针都求出来。我们不妨回顾一下前缀函数的代码实现，而后在其基础上，将一维拓展至二维，得到失配指针的求解。

void getpi(char* s, int pi[])
{
    int n = strlen(s + 1);
    for(int i = 2; i <= n; i++)
    {
        int j = pi[i - 1];
        while(s[i]!=s[j+1] && j)
            j = pi[j];
        if(s[j + 1] == s[i])
            j++;
        pi[i] = j;
    }
}

BFS 中，i - 1 变成了 u，j 因而就等于 fail[u]。为了得到 i，我们穷举字符集（假设是 26 个字母），trie[u][c] 节点就是 i，对应前缀 s[1,i]。s[i]!=s[j+1] 这个条件，j + 1 在二维中就变成了 trie[j][?]，整体条件就变成了，j 节点不存在一个由 c 连出的边，即 trie[j][c] 不存在。

基于 Trie 的构建代码，我们实现了 AC 自动机的构建代码：

int fail[N];
queue<int> q;
void build()
{
    for (int i = 0; i < 26; i++)
        if (trie[0][i])
            q.push(trie[0][i]);
    while (q.size())
    {
        int u = q.front();
        int j = fail[u];
        q.pop();
        for (int c = 0; c < 26; i++)
        {
            while (j && !trie[j][c])
                j = fail[j];
            if (trie[j][c])
                j = trie[j][c];
            fail[trie[u][c]] = j;
        }
    }
}

Trie 图

注意到在匹配过程中，我们需要不断地跳 fail 指针，直到跳到根结点或者存在字符 c 对应的结点。我们可以修改字典树结构，将不存在的字典树的状态链接到了失配指针的对应状态。在原字典树中，每一个结点代表一个字符串 \(S\)，是某个模式串的前缀。而在修改字典树结构后，尽管增加了许多转移关系，但结点（状态）所代表的字符串是不变的。此时的 trie[u][c] 代表的是状态 \(u\) 的后继状态，而不是 \(u\) 的子结点。我们将这种结构称为 Trie 图。

一种比较简单的理解方式是：如果在位置 \(u\) 失配，我们会跳转到 \(\text{fail}[u]\) 的位置。所以我们可能沿着 fail 数组跳转多次才能来到下一个能匹配的位置。所以我们可以用 tr 数组直接记录记录下一个能匹配的位置，这样就能节省下很多时间。

我们将之前的 GIF 图改一下：

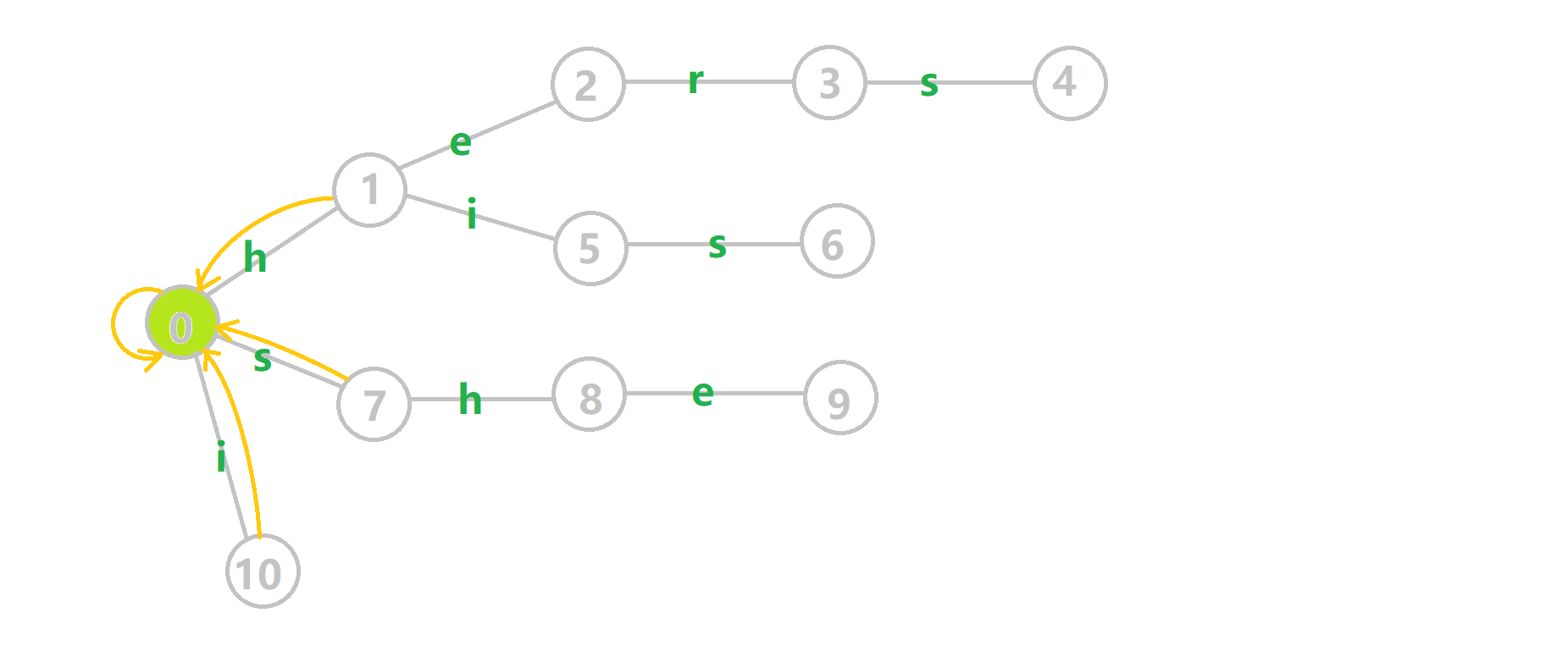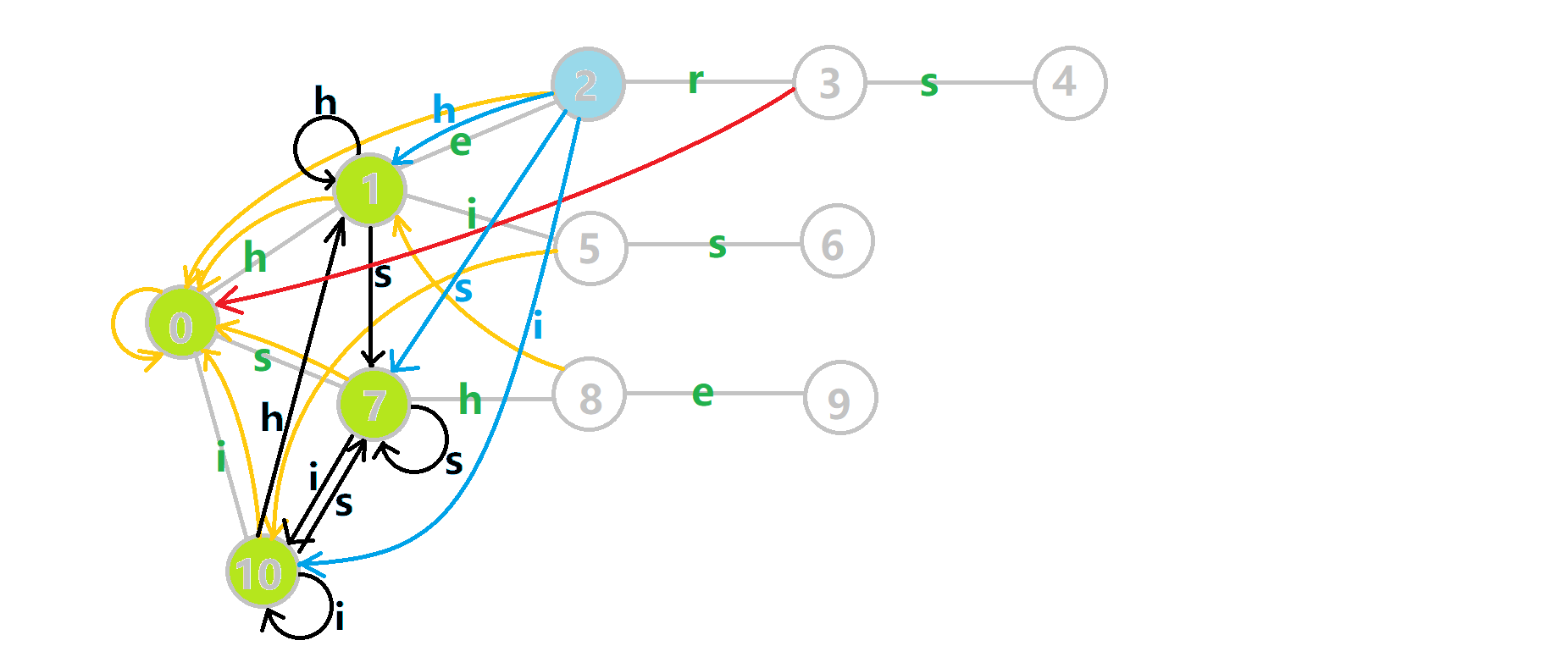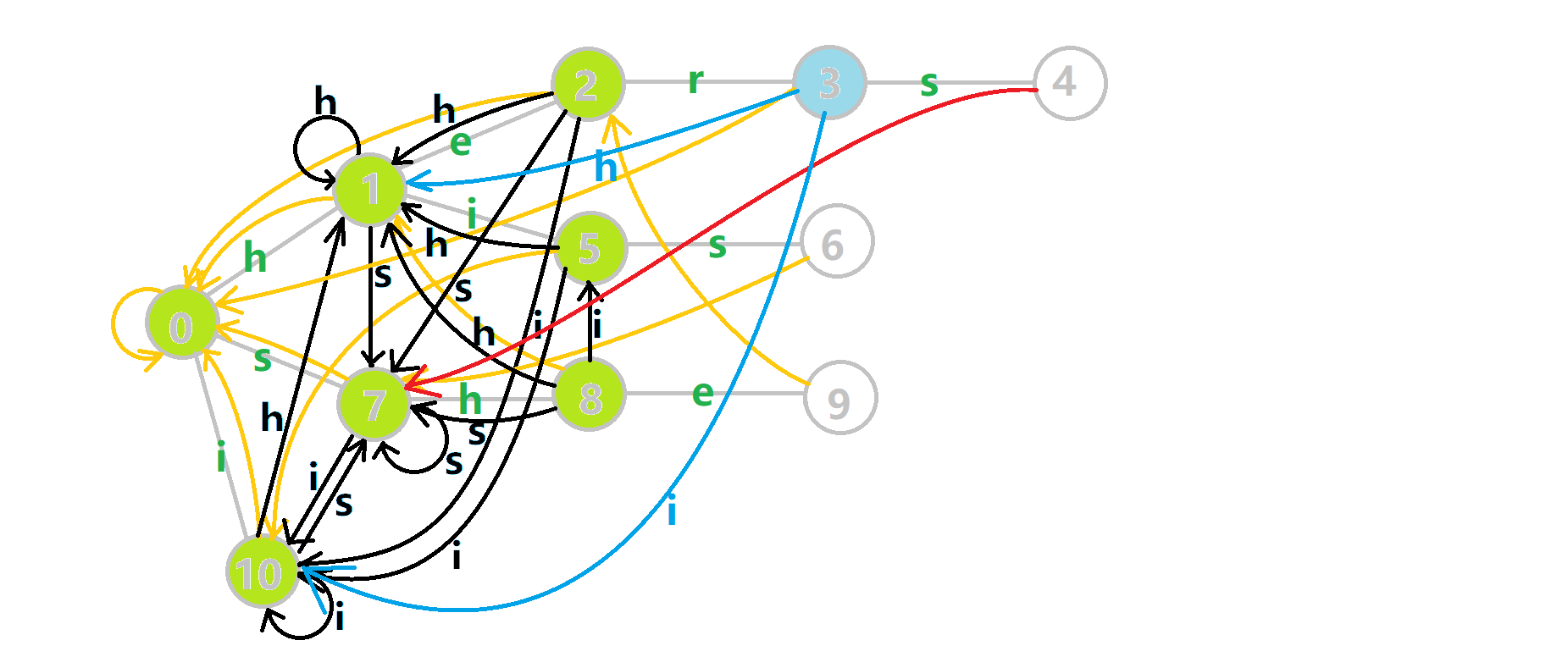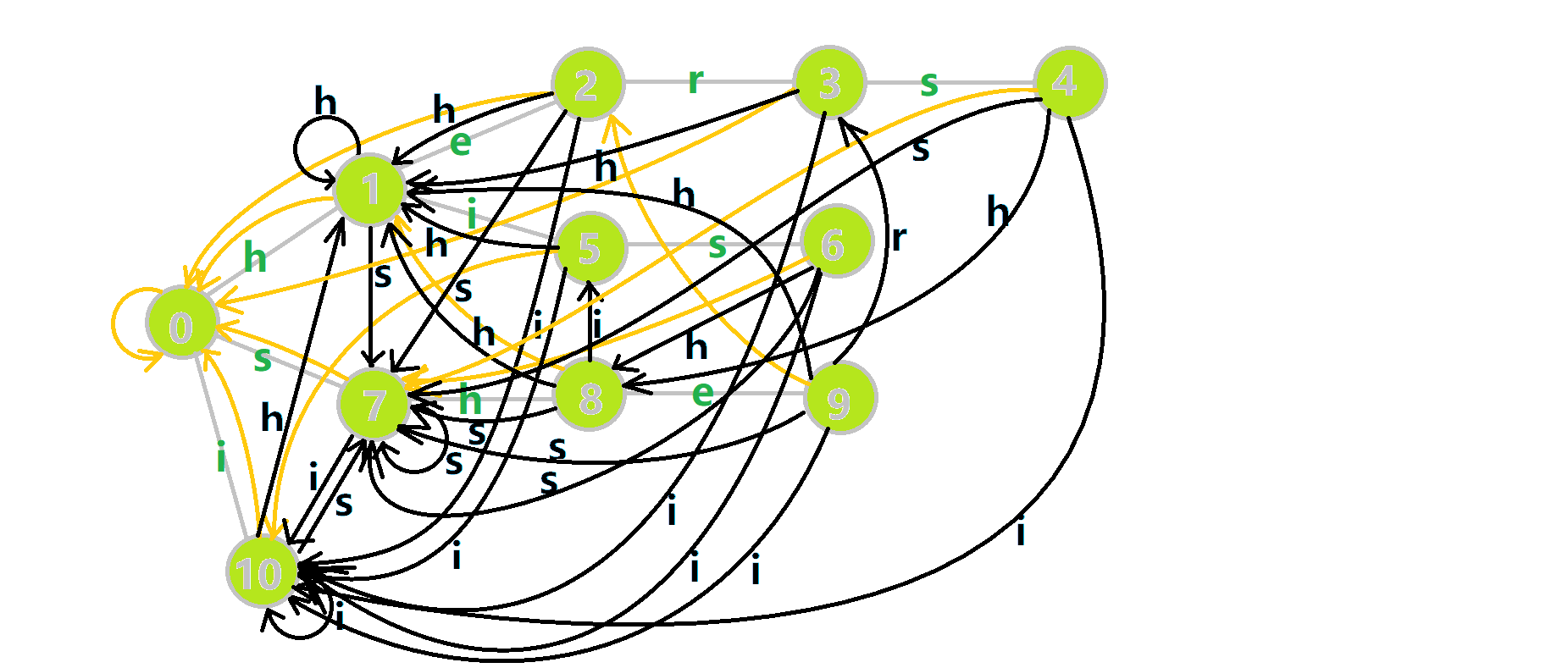
1. 蓝色结点：BFS 遍历到的结点 u
2. 蓝色的边：当前结点下，AC 自动机修改字典树结构连出的边。
3. 黑色的边：AC 自动机修改字典树结构连出的边。
4. 红色的边：当前结点求出的 fail 指针
5. 黄色的边：fail 指针
6. 灰色的边：字典树的边

可以发现，众多交错的黑色边将字典树变成了 字典图。图中省略了连向根结点的黑边（否则会更乱）。我们重点分析一下结点 5 遍历时的情况。我们求 \(\text{trie}[5][s]=6\) 的 fail 指针：

本来的策略是找 fail 指针，于是我们跳到 \(\text{fail}[5]=10\) 发现没有 s 连出的字典树的边，于是跳到 \(\text{fail}[10]=0\)，发现有 \(\text{trie}[0][s]=7\)，于是 \(\text{fail}[6]=7\)；但是有了黑边、蓝边，我们跳到 \(\text{fail}[5]=10\) 之后直接走 \(\text{trie}[10][s]=7\) 就走到 \(7\) 号结点了。

这就是 build 完成的两件事：构建 fail 指针和建立字典图。这个字典图也会在查询的时候起到关键作用。

int fail[N];
queue<int> q;
void build()
{
    for (int i = 0; i < 26; i++)
        if (trie[0][i])
            q.push(trie[0][i]);
    while (q.size())
    {
        int u = q.front();
        int j = fail[u];
        q.pop();
        for (int c = 0; c < 26; i++)
        {
            if (trie[u][c])
                fail[trie[u][c]] = trie[j][c], q.push(trie[u][c]);
            else
                trie[u][c] = trie[j][c];
        }
    }
}

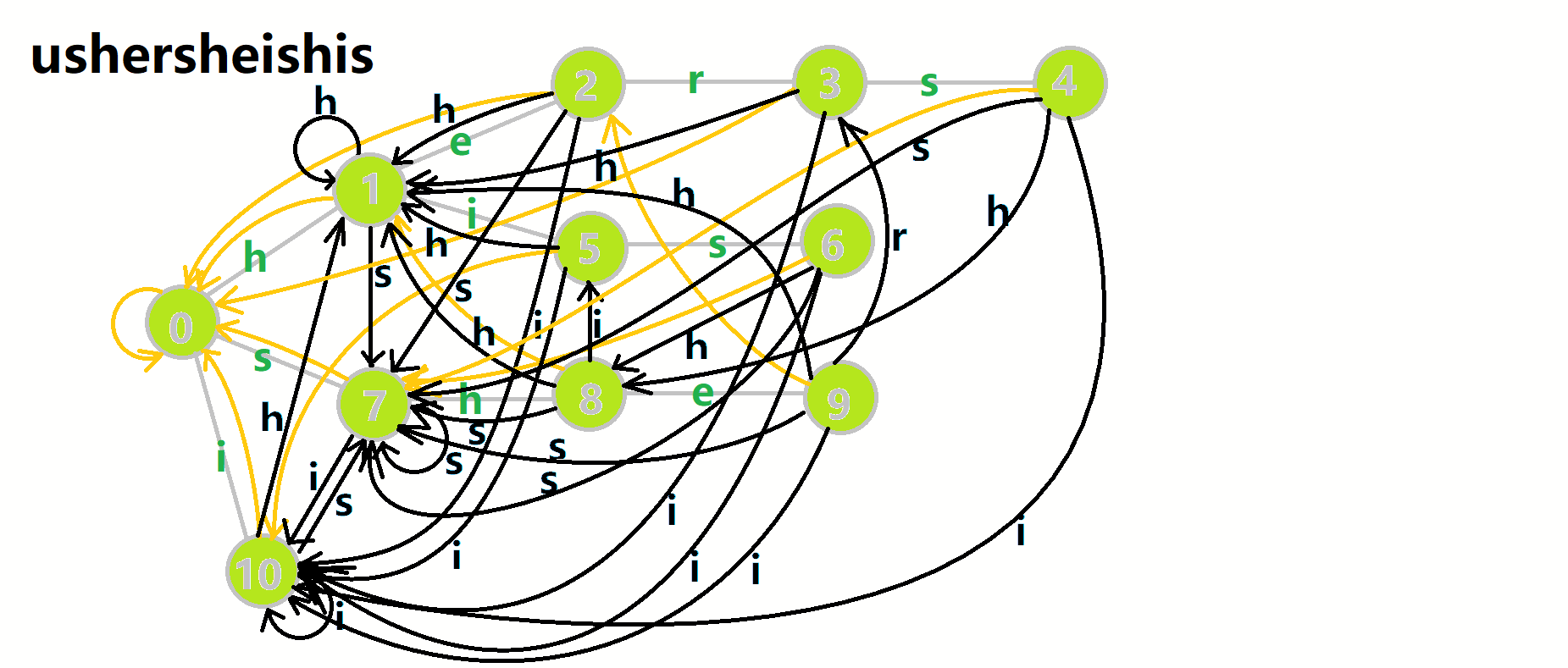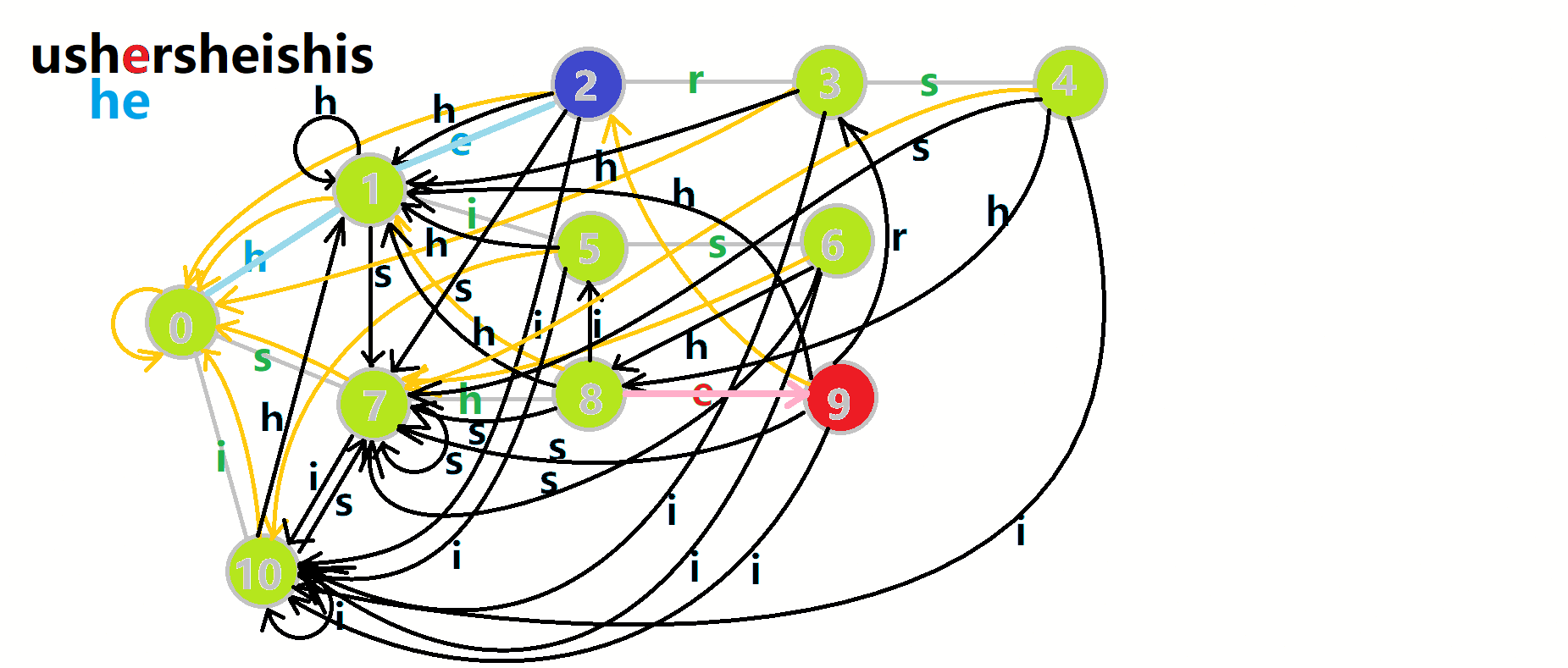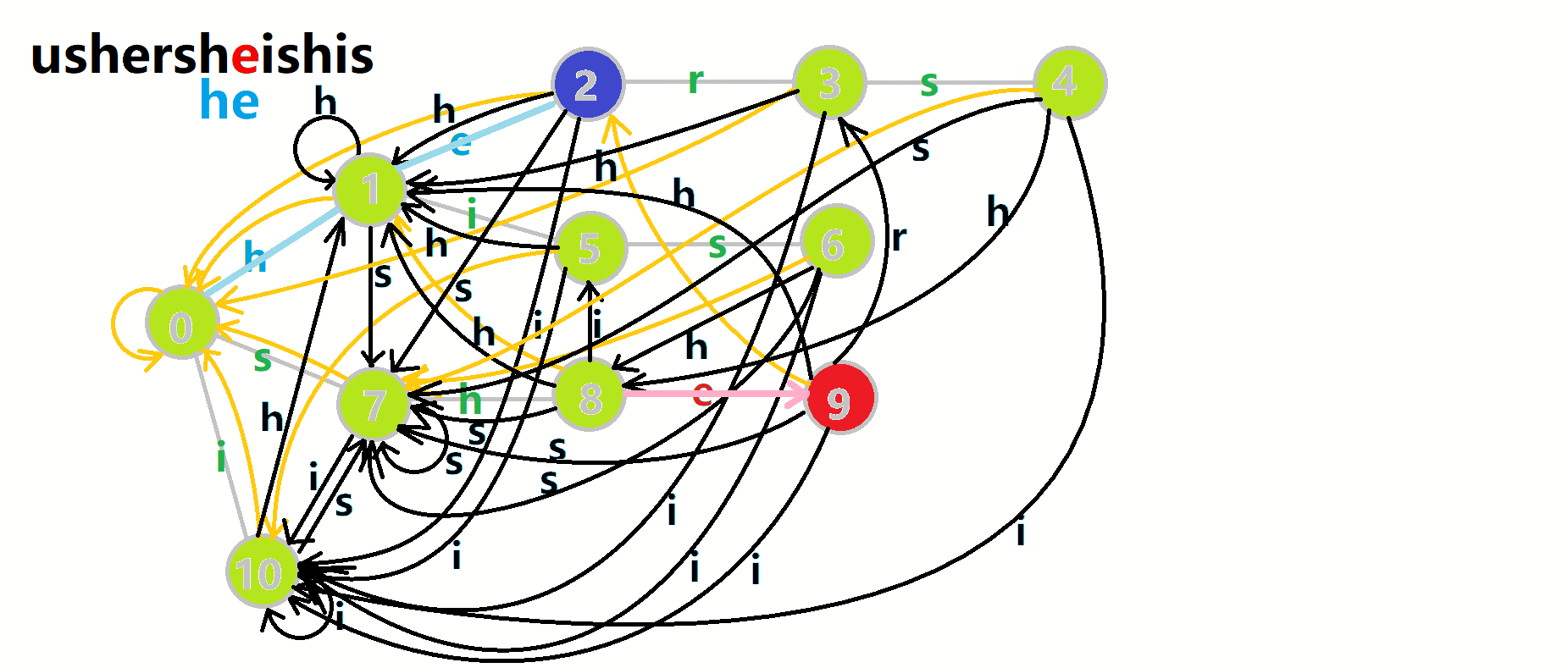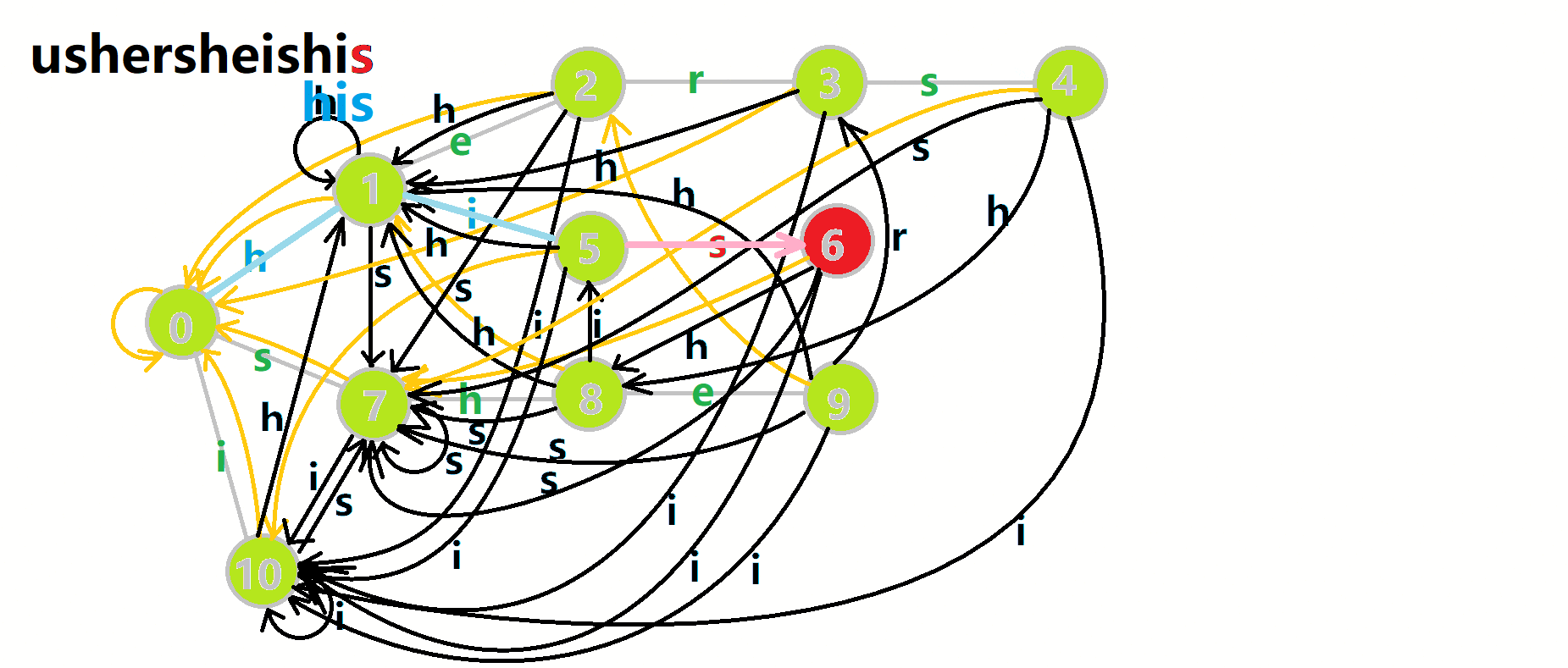
AC 自动机的匹配

我们可以将匹配过程看作是在 Trie 图上的一次遍历，每次遍历都是沿着 fail 指针跳转，直到跳到根结点或者存在字符 c 对应的结点。如果跳到根结点，说明匹配失败，如果跳到存在字符 c 对应的结点，说明匹配成功。

我们从根结点开始尝试匹配 ushersheishis，那么 \(p\) 的变化将是：

1. 红色结点：\(p\) 结点
2. 粉色箭头：\(p\) 在自动机上的跳转，
3. 蓝色的边：成功匹配的模式串
4. 蓝色结点：示跳 fail 指针时的结点（状态）。

当查询为多少个模式串在原串中出现过时，代码如下：

int query(char *s)
{
    int n = strlen(s + 1);
    int u = 0, res = 0;
    for (int i = 1; i <= n; i++)
    {
        int c = s[i] - 'a';
        u = trie[u][c];
        for (int j = u; j && cnt[j] != -1; j = fail[j])
        {
            res += cnt[j];
            cnt[j] = -1;
        }
    }
    return res;
}

例题

模板题-HDU2222

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 1e6 + 10;
int tr[N][26], fail[N], cnt[N];
char str[M];
int idx = 0;
queue<int> q;
inline void insert()
{
    int p = 0;
    for (int i = 1; str[i]; i++)
    {
        int c = str[i] - 'a';
        if (!tr[p][c])
            tr[p][c] = ++idx;
        p = tr[p][c];
    }
    cnt[p]++;
}

inline void build()
{
    for (int i = 0; i < 26; i++)
        if (tr[0][i])
            q.push(tr[0][i]);
    while(!q.empty())
    {
        int t = q.front();
        q.pop();
        for(int i = 0; i < 26; i++)
        {
            if(tr[t][i]) fail[tr[t][i]] = tr[fail[t]][i], q.push(tr[t][i]);
            else tr[t][i] = tr[fail[t]][i];
        }
    }
}

inline int query()
{
    int u = 0, res = 0;
    for(int i = 1; str[i]; i++)
    {
        u = tr[u][str[i] - 'a'];
        for(int j = u; j; j = fail[j])
        res += cnt[j], cnt[j] = 0;
    }
    return res;
}
int main()
{
    int Case;
    scanf("%d", &Case);
    while (Case--)
    {
        memset(tr, 0, sizeof tr);
        memset(fail, 0, sizeof fail);
        memset(cnt, 0, sizeof cnt);
        idx = 0;
        int n;
        scanf("%d", &n);
        for (int i = 0; i < n; i++)
        {
            scanf("%s", str + 1);
            insert();
        }
        build();
        scanf("%s", str + 1);
        printf("%d\n", query());
    }
}

POJ1204-Word Puzzles

题意

给定一个字符矩阵和 k 个字符串, 询问字符串在矩阵中出现的起始位置和字符串方向. （可以斜着构成字符串）

分析

和 AC 自动机的模板相比, 文本串变成了字符矩阵, 但是实际做题的时候把矩阵转换成字符串去做, 但是要注意细节的处理.

• 利用方向向量分 8 个方向去匹配
• 要记录结果可以将模式串反过来构建 Trie 树, 这样匹配到模式串结尾时就是开头的字母.
• 由于建串的时候时反过来建的, 所以我们匹配时候的方向和实际方向是相反的, 可以利用数组一一映射一下.

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int M = 1010, N = 1e6 + 10;
char g[M][M], str[M];
int tr[N][26], idx = 0, fail[N], cnt[N], id[N];
int dx[8] = {-1, -1, 0, 1, 1, 1, 0, -1};
int dy[8] = {0, 1, 1, 1, 0, -1, -1, -1};
int trans[8] = {4, 5, 6, 7, 0, 1, 2, 3};
int n, m, k;
pair<int, int> ans[M];
int dir[M];
inline void insert(int idid)
{
    int p = 0;
    for (int i = strlen(str) - 1; i >= 0; i--)
    {
        int c = str[i] - 'A';
        if (!tr[p][c])
            tr[p][c] = ++idx;
        p = tr[p][c];
    }
    cnt[p]++;
    id[p] = idid;
}

inline void build()
{
    queue<int> q;
    for (int i = 0; i < 26; i++)
        if (tr[0][i])
            q.push(tr[0][i]);
    while (!q.empty())
    {
        int t = q.front();
        q.pop();
        for (int i = 0; i < 26; i++)
        {
            if (tr[t][i])
                fail[tr[t][i]] = tr[fail[t]][i], q.push(tr[t][i]);
            else
                tr[t][i] = tr[fail[t]][i];
        }
    }
}

inline void query(int x, int y, int co)
{
    for (int tx = x, ty = y, j = 0; tx >= 0 && ty >= 0 && tx < n && ty < m; tx += dx[co], ty += dy[co])
    {
        int p = j = tr[j][g[tx][ty] - 'A'];

        while (p)
        {
            if (cnt[p])
            {
                int temp = id[p];
                ans[temp] = {tx, ty};
                dir[temp] = trans[co];
            }
            cnt[p] = 0;
            p = fail[p];
        }
    }
}

int main()
{

    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < n; i++)
        scanf("%s", g[i]);
    for (int i = 0; i < k; i++)
    {
        scanf("%s", str);
        insert(i);
    }
    build();

    for (int i = 0; i < n; i++)
        for (int j = 0; j < 8; j++)
            query(i, 0, j), query(i, m - 1, j);
    for (int i = 0; i < m; i++)
        for (int j = 0; j < 8; j++)
            query(0, i, j), query(n - 1, i, j);
    for (int i = 0; i < k; i++)
        printf("%d %d %c\n", ans[i].first, ans[i].second, dir[i] + 'A');

    return 0;
}

字符串哈希

哈希函数

Hash 的核心思想在于, 将输入映射到一个值域较小、可以方便比较的范围.

我们定义一个把字符串映射到整数的函数 , 这个\(f\)称为是 Hash 函数. 通过这个函数, 我们可以快捷的比较两个字符串是否相等.

我们通常使用多项式哈希的方法, 即\(f(s) = \sum s[i] \times b^i (mod M)\).

从这个函数表达式可以看出, 两个字符串存在不相等却哈希值相等的情况, 哈希函数的判断是一个必要条件, 但是我们可以通过恰当地选取\(b,M\)和多次哈希来尽可能降低冲突率.

哈希函数的实现

通常面对多次询问子串哈希的情况, 我们可以先预处理出每个前缀的哈希值.

令\(f_i(s)\)表示\(f(s[1,i])\), 那么\(f(s[l,r]) = \frac {f_r(s) - f_{l-1}(s)} {b^{l-1}}\)

const int N = 10010, b = 10, M = 1e9 + 9;
char s[N];
int h[N], p[N] = {1};
void init()
{
    int n = strlen(s + 1);
    for(int i = 1; i <= n; i++)
    {
        h[i] = (h[i - 1] * b % M + s[i]) % M;
        p[i] = p[i - 1] * b % M;
    }
}
int gethash(int l, int r)
{
    return ((h[r] - h[l - 1] * p[r - l + 1]) % M + M) % M;
}

哈希的应用

CF898F-Restoring the Expression

题意

在数字串\(s\)中插入一个加号一个等号, 使算式成立, 输出成立的等式.

分析

考虑暴力+优化, 直接枚举加号和等号的位置需要\(O(n^2)\)的复杂度, 高精度加法需要\(O(n)\)的复杂度, 总共是\(O(n^3)\)的复杂度, 显然会 TLE. 所以考虑加法的性质和判断的方法.

• 若右式是一个\(n\)位的数, 那么左式至少有一个数为\(n\)或\(n-1\)位, 较长的数可以在加号左右两侧, 因此\(2 \times 2 = 4\), 对于每一个确定的等号的位置, 加号共有 4 种可能的位置.
• 在确定了加号和等号的位置后, 通过哈希去判断左式和右式是否相等, 因为判断的是必要条件, 所以最好取较大而不常用的模数或者使用双哈希.

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1000010, ba = 10;
const ll mo = 19491001;
char s[N];
ll h[N], b[N] = {1}, ri;
int len, n;

ll gh(int x, int y)
{
    return ((h[y] - h[x - 1] * b[y - x + 1]) % mo + mo) % mo;
}
bool ch(int x, int y)
{
    if (x == 0 || (y - x != 1 && s[x + 1] == '0') || (y != n - 1 && s[y + 1] == '0'))
        return false;
    else
        return true;
}
void print(int x, int y)
{
    for (int i = 1; i <= x; i++)
        printf("%c", s[i]);
    putchar('+');
    for (int i = x + 1; i <= y; i++)
        printf("%c", s[i]);
    putchar('=');
    for (int i = y + 1; i <= n; i++)
        printf("%c", s[i]);
}
int main()
{
    scanf("%s", s + 1);
    n = strlen(s + 1);
    for (int i = 1; i <= n; i++)
    {
        h[i] = (h[i - 1] * ba % mo + s[i] - '0') % mo;
        b[i] = b[i - 1] * ba % mo;
    }
    int nn = n - n / 3;
    for (int i = n >> 1; i <= nn; i++)
    {
        if(i + i < n) continue;
        ri = gh(i + 1, n), len = n - i;
        if (ch(len, i) && (gh(1, len) + gh(len + 1, i)) % mo == ri)
        {
            print(len, i);
            return 0;
        }
        if (ch(len - 1, i) && (gh(1, len - 1) + gh(len, i)) % mo == ri)
        {
            print(len - 1, i);
            return 0;
        }
        if (ch(i - len, i) && (gh(1, i - len) + gh(i - len + 1, i)) % mo == ri)
        {
            print(i - len, i);
            return 0;
        }
        if (ch(i - len + 1, i) && (gh(1, i - len + 1) + gh(i - len + 2, i)) % mo == ri)
        {
            print(i - len + 1, i);
            return 0;
        }
    }
}

CF985F-Isomorphic Strings

题意

给定一个字符串\(s\), 执行\(m\)次询问, 每次询问判断\(s\)的两个子串是否同构. 对于两个字符串同构的定义可以概括为: 如果\(s\)中的字符可以被替换得到\(t\), 那么这两个字符串是同构的. 所有出现的字符都必须用另一个字符替换, 同时保留字符的顺序. 两个字符不能映射到同一个字符上, 但字符可以映射自己本身.

分析

一开始做这道题首先想到的是用两个 map 去完成. 从前向后遍历字符串, 如果是首次出现一个字母, 就记录这个字母和对应位置上另一个字符串的字母, 如果不是首次出现, 就去判断这个字母对应的字母和存的字母是否相同. 对于两个字符串各做一遍上述操作, 如果没有产生矛盾, 就判断为同构, 否则不同同构. 根据数据范围, 考虑最糟糕的情况是\(m\)次询问全部是针对\(s\)整个串, 最终最坏复杂度为\(O(nm)\), 最终会 TLE.

那么考虑正解, 个人感觉这道题的正解从位运算绕一下理解更方便. 首先, \(s\)只由 26 个小写英文字母组成, 其次, 我们只需要判断是否同构而不需要知道对于每次判断而言字母之间的映射关系. 基于这两点, 我们考虑这样一个做法:

对于 26 个字母, 构造 26 个 01 串, 对于每个字母, 遍历\(s\), 如果\(s[i]\)与该字母相同则为 1, 否则为 0. 而后, 我们可以将这 26 个字符串转换成十进制的数. 对于判断同构串时, 构造的两组 01 串转化后, 如果存在两个数对应相等, 那么说明这两个数代表的字母的对应位置在两串中完全一致, 也就是符合同构的条件. 那么, 我们只需要判断两组数是否完全相等就可以了.

但是, 此时考虑到两组 01 串每个长度可以长达\(2 \times 10^5\), 所以转换成十进制的数存不下, 所以我们想到可以直接利用哈希去判断两组 01 串是否相等.

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200010;
const ll mod = 1e9 + 7, B = 233;
ll h[26][N], p[N] = {1ll};
char S[N];
int main()
{
    int n, m, x, y, l;
    scanf("%d%d", &n, &m);
    getchar();
    scanf("%s", S + 1);
    for (int i = 1; i <= n; i++)
        p[i] = p[i - 1] * B % mod;
    for (int i = 0; i < 26; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            h[i][j] = (h[i][j - 1] * B + (long long)(S[j] == i + 'a')) % mod;
        }
    }
    while (m--)
    {
        scanf("%d%d%d", &x, &y, &l);
        vector<int> v1, v2;
        for (int i = 0; i < 26; ++i)
        {
            v1.push_back(((h[i][x + l - 1] - p[l] * h[i][x - 1]) % mod + mod) % mod);
            v2.push_back(((h[i][y + l - 1] - p[l] * h[i][y - 1]) % mod + mod) % mod);
        }
        sort(v1.begin(), v1.end());
        sort(v2.begin(), v2.end());
        printf("%s\n", v1 == v2 ? "YES" : "NO");
    }
}

CF985F-Isomorphic Strings

题意

给定一个字符串\(s\), 执行\(m\)次询问, 每次询问判断\(s\)的两个子串是否同构. 对于两个字符串同构的定义可以概括为: 如果\(s\)中的字符可以被替换得到\(t\), 那么这两个字符串是同构的. 所有出现的字符都必须用另一个字符替换, 同时保留字符的顺序. 两个字符不能映射到同一个字符上, 但字符可以映射自己本身.

分析

一开始做这道题首先想到的是用两个 map 去完成. 从前向后遍历字符串, 如果是首次出现一个字母, 就记录这个字母和对应位置上另一个字符串的字母, 如果不是首次出现, 就去判断这个字母对应的字母和存的字母是否相同. 对于两个字符串各做一遍上述操作, 如果没有产生矛盾, 就判断为同构, 否则不同同构. 根据数据范围, 考虑最糟糕的情况是\(m\)次询问全部是针对\(s\)整个串, 最终最坏复杂度为\(O(nm)\), 最终会 TLE.

那么考虑正解, 个人感觉这道题的正解从位运算绕一下理解更方便. 首先, \(s\)只由 26 个小写英文字母组成, 其次, 我们只需要判断是否同构而不需要知道对于每次判断而言字母之间的映射关系. 基于这两点, 我们考虑这样一个做法:

对于 26 个字母, 构造 26 个 01 串, 对于每个字母, 遍历\(s\), 如果\(s[i]\)与该字母相同则为 1, 否则为 0. 而后, 我们可以将这 26 个字符串转换成十进制的数. 对于判断同构串时, 构造的两组 01 串转化后, 如果存在两个数对应相等, 那么说明这两个数代表的字母的对应位置在两串中完全一致, 也就是符合同构的条件. 那么, 我们只需要判断两组数是否完全相等就可以了.

但是, 此时考虑到两组 01 串每个长度可以长达\(2 \times 10^5\), 所以转换成十进制的数存不下, 所以我们想到可以直接利用哈希去判断两组 01 串是否相等.

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200010;
const ll mod = 1e9 + 7, B = 233;
ll h[26][N], p[N] = {1ll};
char S[N];
int main()
{
    int n, m, x, y, l;
    scanf("%d%d", &n, &m);
    getchar();
    scanf("%s", S + 1);
    for (int i = 1; i <= n; i++)
        p[i] = p[i - 1] * B % mod;
    for (int i = 0; i < 26; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            h[i][j] = (h[i][j - 1] * B + (long long)(S[j] == i + 'a')) % mod;
        }
    }
    while (m--)
    {
        scanf("%d%d%d", &x, &y, &l);
        vector<int> v1, v2;
        for (int i = 0; i < 26; ++i)
        {
            v1.push_back(((h[i][x + l - 1] - p[l] * h[i][x - 1]) % mod + mod) % mod);
            v2.push_back(((h[i][y + l - 1] - p[l] * h[i][y - 1]) % mod + mod) % mod);
        }
        sort(v1.begin(), v1.end());
        sort(v2.begin(), v2.end());
        printf("%s\n", v1 == v2 ? "YES" : "NO");
    }
}

CF961F-k-substrings

题意

给定一个字符串\(s\), 每次从左右两端去除一个字母, 构造出\(\lceil \frac {|s|} 2 \rceil\)个子串, 对于每个子串, 求解它的最长公共前后缀的长度.

分析

如果是构造完了去求解最长公共前后缀的长度, 复杂度是\(O(n^2)\), 会 TLE. 但是考虑这个暴力的做法中, 每次求解的时候会有额外信息提供, 所以考虑递推的思想.

设答案序列为\(ans[1...{\lceil \frac {|s|} 2 \rceil}]\), 考虑\(ans[i+1]\), \(i+1\)相较于\(i\)号子串, 左右两端各少一个字母, 所以即使\(i+1\)号子串前缀加后缀就是这个子串本身, \(ans[i+1]\)相较于\(ans[i]\)也至少小 2.

根据这样的规律, 我们可以倒着去做, 从中间开始计算, 每次向两边扩展一个字母, 枚举\(ans[i+1]+2,ans[i+1], ans[i+1]-2,...,-1\), 只要长度符合前后缀条件就不再循环直接记录答案.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1000010;
const ll B = 233, mod = 1e9 + 7;
char s[N];
int n, cnt, l, r, ans[N];
ll h[N], p[N] = {1ll};
ll gethash(int l, int r)
{
    return ((h[r] - h[l - 1] * p[r - l + 1]) % mod + mod) % mod;
}
int main()
{
    scanf("%d", &n);
    getchar();
    scanf("%s", s + 1);
    for (int i = 1; i <= n; i++)
    {
        p[i] = p[i - 1] * B % mod;
        h[i] = (h[i - 1] * B % mod + s[i]) % mod;
    }
    cnt = n + 1 >> 1;
    if (n & 1)
        ans[cnt] = -1, l = r = cnt;
    else
    {
        l = cnt, r = cnt + 1;
        if(s[l] == s[r]) ans[cnt] = 1;
        else ans[cnt] = -1;
    }
    for(int i = cnt - 1; i > 0; i--)
    {
        l--, r++;
        for(int j = ans[i + 1] + 2; j >= -1; j -= 2)
        {
            if(j == -1 || gethash(l, l + j - 1) == gethash(r - j + 1, r))
            {
                ans[i] = j;
                break;
            }
        }
    }

    for(int i = 1; i <= cnt; i++) printf("%d ", ans[i]);
    return 0;
}

BZOJ3916-Friends

题意

对于字符串\(S\), 先复制一遍接在\(S\)尾部, 然后再在任意位置插入一个字符, 给定构造好的字符串\(T\), 求原字符串\(S\).

分析

首先设\(T\)长度为\(n\), 如果\(n\)为偶数, 那么必然不存在原串, 因为一个字符串长度乘二加一必然是奇数, 然后, 可以知道原串的长度一定是\(\frac n 2\).

根据这两个结论, 我们可以直接枚举每个位置是否是插入的字符, 通过哈希去验证去除该字符后剩下的是否是两个完全相同的串, 枚举复杂度为\(O(n)\), 验证复杂度为\(O(1)\), 总体复杂度为\(O(n)\), 符合题目要求.

note: 求解去除一个字符后的哈希值卡了好久, 总而言之是从哈希的定义式出发考虑, 举例好理解一点.

代码

#include <cstdio>
using namespace std;
typedef long long ll;
const int N = 2000010;
const int B = 233, mod = 1e9 + 7;
unsigned int x, y, bp, h[N], p[N] = {1};
int n, haf, pos;
char s[N];
bool flag = false;
ll gethash(int l, int r)
{
    return (h[r] - h[l - 1] * p[r - l + 1]);
}
int main()
{
    scanf("%d%s", &n, s + 1);
    haf = n / 2;
    if (!(n % 2))
    {
        puts("NOT POSSIBLE");
        return 0;
    }
    for (int i = 1; i <= n; i++)
    {
        p[i] = p[i - 1] * B;
        h[i] = (h[i - 1] * B + s[i]);
    }
    for (int i = 1; i <= n; i++)
    {
        if (i <= haf)
            x = h[haf + 1] - h[i] * p[haf - i + 1] + h[i - 1] * p[haf - i + 1];
        else
            x = h[haf];
        if (i <= haf + 1)
            y = h[n] - h[haf + 1] * p[haf];
        else
            y = h[n] - h[i] * p[n - i] + (h[i - 1] - h[haf] * p[i - haf - 1]) * p[n - i];
        if (x == y)
        {
            if (flag && bp != x)
            {
                puts("NOT UNIQUE");
                return 0;
            }
            flag = true, bp = x, pos = i;
        }
    }
    if (!flag)
    {
        puts("NOT POSSIBLE");
        return 0;
    }
    for (int i = 1, len = 1; len <= haf; i++)
        if (i != pos)
            printf("%c", s[i]), len++;
    return 0;
}

Matrix Matcher

题意

给定一大一小两个字符矩阵, 问小矩阵在大矩阵中出现的次数.

分析

二维哈希的模板题. 具体而言, 二维哈希的思想是先对每一列元素进行哈希, 降维成一维后再进行一次哈希, 最终得到的这个值就是这个矩阵的哈希值. 我们同样可以利用类似于前缀和的方法去优化查询.

代码

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const ull B1 = 131, B2 = 13331;
const int N = 1010;
char s[N][N];
ull h1[N][N], h2[N][N], p1[N * N] = {1ull}, p2[N * N] = {1ull};
int n, m, x, y, T, res = 0;

ull get_hash(ull h[][N], int x1, int y1, int x2, int y2)
{
    return h[x2][y2] - h[x1 - 1][y2] * p1[x2 - x1 + 1] - h[x2][y1 - 1] * p2[y2 - y1 + 1] + h[x1 - 1][y1 - 1] * p1[x2 - x1 + 1] * p2[y2 - y1 + 1];
}

int main()
{
    for (int i = 1; i < N * N; i++)
        p1[i] = p1[i - 1] * B1, p2[i] = p2[i - 1] * B2;
    scanf("%d", &T);
    while (T--)
    {
        res = 0;
        memset(h1, 0, sizeof h1);
        memset(h2, 0, sizeof h2);

        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++)
            scanf("%s", s[i] + 1);
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                h1[i][j] = h1[i - 1][j] * B1 + h1[i][j - 1] * B2 - h1[i - 1][j - 1] * B1 * B2 + s[i][j];
            }
        }

        scanf("%d%d", &x, &y);
        for (int i = 1; i <= x; i++)
            scanf("%s", s[i] + 1);
        for (int i = 1; i <= x; i++)
        {
            for (int j = 1; j <= y; j++)
            {
                h2[i][j] = h2[i - 1][j] * B1 + h2[i][j - 1] * B2 - h2[i - 1][j - 1] * B1 * B2 + s[i][j];
            }
        }

        for (int i = 1; i <= n - x + 1; i++)
            for (int j = 1; j <= m - y + 1; j++)
                if (get_hash(h1, i, j, i + x - 1, j + y - 1) == h2[x][y])
                    res++;

        printf("%d\n", res);
    }
}

CF1096D-Easy Problem

题意

给定字符串\(s\), 要求删去一些字符, 使得\(s\)中不包含"hard"子序列, 给定删去每个字符所需的代价, 求最小代价.

分析

最优解问题, 考虑 DP. 设\(f[i][j]\)表示为了使前\(i\)个字符中不包含\(hard[1,j]\)子序列的代价. 具体而言, \(f[3][2]\)表示前 3 个字符花费了这么多的代价, 使得前 3 个字符不存在"ha"的任何前缀.

状态转移方程:

\[ \begin{eqnarray} f[i][j] = \begin{cases} f[i-1][j], &s[i] \not = hard[j]\\ min(f[i][j-1]+a[i], f[i-1][j-1]), & s[i] = hard[j] \end{cases} \end{eqnarray} \]

答案: \(min \left\{ f[n][i] \right\}\)

优化: 看到 cf 上 dalao 写的滚动数组, 只需要 f[5]就可以完成.

代码

#include <bits/stdc++.h>
using namespace std;
long long n, a, dp[100010][10], ans;
char hard[5] = {'\0', 'h', 'a', 'r', 'd'}, s[100010];
int main()
{
    scanf("%lld%s", &n, s + 1);
    memset(dp, 0x7f, sizeof(dp));
    for (int i = 1; i <= 4; i++)
    {
        dp[0][i] = 0;
    }
    for (int i = 1; i <= n; i++)
    {
        scanf("%lld", &a);
        for (int j = 1; j <= 4; j++)
        {
            if (s[i] != hard[j])
                dp[i][j] = dp[i - 1][j];
            else
                dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j] + a);
        }
    }
    ans = dp[n][1];
    for (int i = 2; i <= 4; i++)
        ans = min(ans, dp[n][i]);

    printf("%lld\n", ans);
}

POJ3356-AGTC

题意

给定字符串\(a,b\), 给定三种操作: 1）删除\(a\)的某一个字符, 2）在某个位置插入字符, 3）替换\(a\)的某一个字符. 求最少操作次数.

分析

最短编辑距离的模板题.

定义状态:

\(f[i][j]\)表示\(a\)中前\(i\)个字符变成\(b\)中前\(j\)个字符所需要的最小代价.

状态转移:

• 先考虑删除和插入操作, \(f[i][j] = min(f[i-1][j]+1,f[i][j-1]+1)\)
• 如果\(a[i]=b[j]\), 则不需要替换, \(f[i][j] = min(f[i][j],f[i-1][j-1])\)
• 否则, 需要替换这个字服, \(f[i][j] = min(f[i][j],f[i-1][j-1]+1)\)

边界:

\(f[0][j],f[i][0]\)表示变为空串所需要的代价, 代价一定为非空串的长度

#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int n, m, f[N][N];
char a[N], b[N];
int main()
{
    while (scanf("%d%s%d%s", &n, a + 1, &m, b + 1) != EOF)
    {
        memset(f, 0, sizeof(f));
        for (int i = 1; i <= n; i++)
            f[i][0] = i;
        for (int i = 1; i <= m; i++)
            f[0][i] = i;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
                if (a[i] == b[j])
                    f[i][j] = min(f[i][j], f[i - 1][j - 1]);
                else
                    f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
            }
        }
        printf("%d\n", f[n][m]);
    }

    return 0;
}

参考

blb 的博客: https://blog.0xfaner.site/

OI-Wiki: https://oi-wiki.org/